
In the realm of algebra, the ability to simplify expressions containing exponents is not merely a skill but a fundamental necessity for students and professionals alike. Exponent simplification, when mastered, reveals the elegance and efficiency of mathematical expression, allowing for the concise conveyance of complex operations. Grasping the rules that govern exponent manipulation—such as the product, quotient, and power rules, along with dealing with zero and negative exponents—is akin to acquiring a linguistic fluency that enables one to navigate the intricate syntax of algebraic language with ease. This discussion commences with the intention to elucidate these principles, aiming to equip the reader with the proficiency to address algebraic challenges with a heightened sense of confidence. As we prepare to embark on a closer examination of these rules, one must ponder: what insights might we gain from a thorough understanding of these concepts, and how might they illuminate the path to solving more intricate mathematical problems?
Key Takeaways
- Exponents represent repeated multiplication of a base number.
- The product rule states that when multiplying two powers with the same base, the exponents are added.
- The quotient rule states that when dividing two powers with the same base, the exponents are subtracted.
- The power of a power rule involves raising an exponential expression to an additional exponent.
Understanding the Exponent Basics
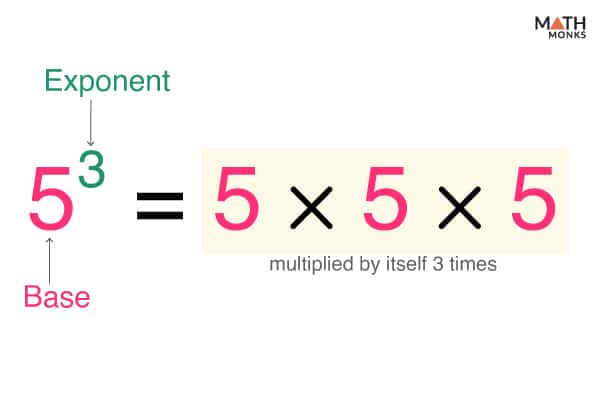
Grasping the fundamental principles of exponents is crucial for simplifying algebraic expressions effectively and accurately. Exponents, also known as powers, are shorthand notations that represent repeated multiplication of a base number. The exponentiation process consists of two components: the base, which is the number being multiplied by itself, and the exponent, which indicates how many times the base is used as a factor.
For instance, 3^4 denotes 3 multiplied by itself 4 times (3 × 3 × 3 × 3). A vital rule is that any non-zero number raised to the power of zero equals one. This concept is essential in simplification processes as it often reduces complex expressions to simpler forms.
Moreover, understanding how to manipulate expressions with exponents involves mastering specific laws, such as the product rule, which states that when multiplying two powers with the same base, one adds the exponents (x^a × x^b = x^(a+b)). Conversely, the quotient rule dictates that when dividing, one subtracts the exponents (x^a ÷ x^b = x^(a-b)). There are also rules for raising powers to powers and for dealing with negative exponents.
Methodical application of these rules enables the simplification of algebraic expressions containing exponents, paving the way for solving more complex mathematical problems.
Read More About: Key Insights: Statistical Significance in Probability and Statistics
Applying the Product Rule
Building on our understanding of exponent basics, let us now explore the product rule, a foundational concept for multiplying algebraic expressions with like bases. This rule states that when you multiply two exponents with the same base, you simply add the exponents. Symbolically, this is expressed as a^m * a^n = a^(m+n). This operation is essential for simplifying expressions and solving equations involving exponents.
The product rule is not just a mechanical process; it is a reflection of repeated multiplication. For example, a^2 * a^3 is essentially saying “a squared times a cubed”, which is the same as multiplying five a’s together (a * a * a * a * a), resulting in a^5.
To elucidate this concept, consider the following table that demonstrates the application of the product rule with various bases and exponents:
Base (a)Exponent 1 (m)Exponent 2 (n)Product Rule ApplicationResulting Exponent (m+n)x23x^2 * x^3x^5y41y^4 * y^1y^5z62z^6 * z^2z^8w33w^3 * w^3w^6v50v^5 * v^0v^5
Educators and students must grasp the product rule for its frequent use in algebra and higher mathematics. It simplifies complex expressions and serves as a stepping stone to more advanced exponent rules.
Dividing With the Quotient Rule
Transitioning from multiplication to division, we encounter the quotient rule, which guides the simplification of expressions when dividing exponents with the same base. To comprehend this rule, consider two exponents with the same base being divided: ( a^m div a^n ), where ( a ) is a nonzero base, and ( m ) and ( n ) are integers. The quotient rule instructs that we subtract the exponent in the denominator from the exponent in the numerator: ( a^m div a^n = a^{m-n} ).
Methodically, let’s examine the process:
- Identify the common base in both the numerator and the denominator.
- Confirm that the base is not zero since ( a^0 ) is undefined for ( a = 0 ).
- Subtract the lower exponent from the higher exponent.
- Write the result with the base raised to this difference in exponents.
For example, to simplify ( x^7 div x^2 ), subtract 2 from 7 to obtain ( x^{7-2} ), which simplifies to ( x^5 ).
The quotient rule is pivotal for solving algebraic problems efficiently. It streamlines the process of dividing expressions and serves as the foundation for more advanced concepts in algebra, such as solving exponential equations. Remember, when the bases are different, or when variables are involved, the quotient rule does not apply directly and further algebraic manipulation may be required.
You Might Like: New IB Maths Curriculum, Changes And Impact
Power of a Power Simplification
Moving beyond the quotient rule, we encounter another fundamental principle of exponents: the power of a power simplification, which involves raising an exponential expression to an additional exponent. This operation is critical for students to master in order to efficiently manage more complex algebraic expressions encountered in higher mathematics.
The rule for simplifying a power of a power is straightforward: when an exponential expression is raised to another power, the exponents are multiplied. Mathematically, this is represented as ((a^m)^n = a^{m cdot n}), where (a) is the base and (m) and (n) are the exponents. This law reflects the repetitive nature of exponentiation as a series of multiplications.
For pedagogical clarity, consider the expression ((x^2)^3). According to the power of a power rule, you would multiply the exponents, resulting in (x^{2 cdot 3}), which simplifies to (x^6). This is the equivalent of (x^2 cdot x^2 cdot x^2), showcasing the repeated multiplication inherent in exponentiation.
It’s essential to methodically apply this rule, ensuring that the base remains unchanged while the exponents undergo multiplication. Consequently, students must distinguish between the multiplication of bases and the multiplication of exponents, which are governed by separate rules. Mastery of power of a power simplification paves the way for tackling more advanced exponential operations with confidence.
Working With Zero and Negative Exponents
Delving into the realm of zero and negative exponents reveals essential concepts that further expand our understanding of algebraic expressions and their simplifications. Zero exponents, according to the laws of exponents, render any non-zero base raised to the power of zero equal to one. This rule, (a^0 = 1) (where (a ≠ 0)), is pivotal as it simplifies expressions and serves as a foundational concept for more advanced operations.
When dealing with negative exponents, the key is to recall that they denote the reciprocal of the base raised to the positive opposite of the given exponent. Therefore, (a^{-n} = rac{1}{a^n}), where (a ≠ 0). This transformation from a negative to a positive exponent is crucial in the simplification process, turning division into multiplication by a fraction.
In practice, these principles enable us to convert expressions with negative exponents into their positive counterparts, which are often more intuitive to work with. For instance, (x^{-3}) becomes ( rac{1}{x^3}), and (y^{-1}) simplifies to ( rac{1}{y}). Mastery of zero and negative exponents is essential for students to effectively simplify and manipulate algebraic expressions involving powers, preparing them for more complex algebraic challenges ahead.
Read Also: Ultimate comparison Between IB Math AA Vs Math AI
Frequently Asked Questions
How Does the Concept of Exponent Simplification Apply to Complex Numbers, and What Are the Specific Rules for Simplifying Powers of Complex Numbers?
Exponent simplification in the realm of complex numbers adheres to fundamental algebraic principles, with specific rules accommodating complex components. When simplifying powers of complex numbers, one must apply the power to both the real and imaginary parts, often utilizing Euler’s formula. This aids in converting complex exponents into a trigonometric form that can be more easily manipulated, ensuring accuracy and consistency in simplification while maintaining the integrity of the complex number’s structure.
In What Ways Can Exponent Simplification Be Helpful in Solving Logarithmic Equations, Given That Exponents and Logarithms Are Inverse Operations?
Exponent simplification facilitates solving logarithmic equations by translating exponential forms to logarithmic forms and vice versa, leveraging their inverse nature. This process allows for the isolation and solving of variables within logarithmic equations. Understanding the properties of exponents, such as the power and product rules, enables one to adeptly manipulate and simplify expressions, ultimately streamlining the solution of logarithmic equations encountered in various mathematical and applied contexts.
How Do the Rules of Exponent Simplification Change When Dealing With Exponential Expressions in Modular Arithmetic or Other Non-Standard Number Systems?
In modular arithmetic and non-standard number systems, exponent simplification rules must be adapted to account for unique properties. For instance, in modular arithmetic, exponents are evaluated using modular exponentiation which can lead to different simplifications than in standard arithmetic. Similarly, alternative number systems may require distinct approaches to exponentiation, impacting simplification techniques. It’s crucial to understand the underlying rules of the system in use to correctly simplify exponential expressions.
Can Exponent Simplification Techniques Be Extended to Help Simplify Expressions Involving Infinite Series or Sequences With Exponential Terms?
Exponent simplification techniques are not directly extendable to infinite series or sequences with exponential terms, due to the complexity and convergence considerations inherent in such expressions. Traditional exponent rules apply to finite algebraic expressions and do not account for the summation or limit processes required in analyzing infinite series. Therefore, simplification in this context typically involves additional mathematical tools from analysis, such as convergence tests and power series manipulation strategies.
What Are Some Common Mistakes Students Make When Attempting to Simplify Algebraic Expressions With Exponents That Involve Multiple Variables, and How Can These Be Avoided?
Common mistakes when simplifying expressions with exponents and multiple variables include misapplying exponent rules and combining unlike terms. To avoid these, students should methodically apply the laws of exponents step by step, ensure variables match when combining terms, and double-check their work for accuracy. It is essential to maintain a structured approach, keeping operations with similar bases together and treating each variable distinctly to prevent errors in simplification.
Conclusion
[VERY SHORT 75 WORD CONCLUSION]:
In conclusion, mastery of exponent simplification is a fundamental aspect of algebra that enhances mathematical literacy. By comprehending the basic rules for exponents and applying them through the product, quotient, and power rules, as well as understanding the special cases of zero and negative exponents, one can efficiently manipulate algebraic expressions. This proficiency allows for the simplification of complex equations, thereby facilitating a deeper understanding of algebraic concepts and problem-solving techniques.
